Which Key Mechanism: Securely Generating a Symmetric Key for Two-Party Data Exchange?

The key used by two parties to securely generate a symmetric key for data encryption is called a “Diffie-Hellman key.”

In today’s world of constant digital communication, ensuring security is paramount. One of the foundational techniques to secure these communications is the Diffie-Hellman Key Exchange. This innovative algorithm is employed worldwide to secure countless online transactions and communications.

Understanding the Basics

At its core, the Diffie-Hellman Key Exchange is a method that allows two parties to each independently create a shared secret, even while communicating over an insecure channel. This shared secret can subsequently be employed as a symmetric key for encrypted communication between the parties.

Historical Context

The Diffie-Hellman Key Exchange, introduced by Whitfield Diffie and Martin Hellman in 1976, revolutionized the field of cryptography. Before this, encryption and decryption were typically achieved using the same key, which necessitated the secure exchange of this key between parties, posing a significant challenge.

How Does Diffie-Hellman Work?

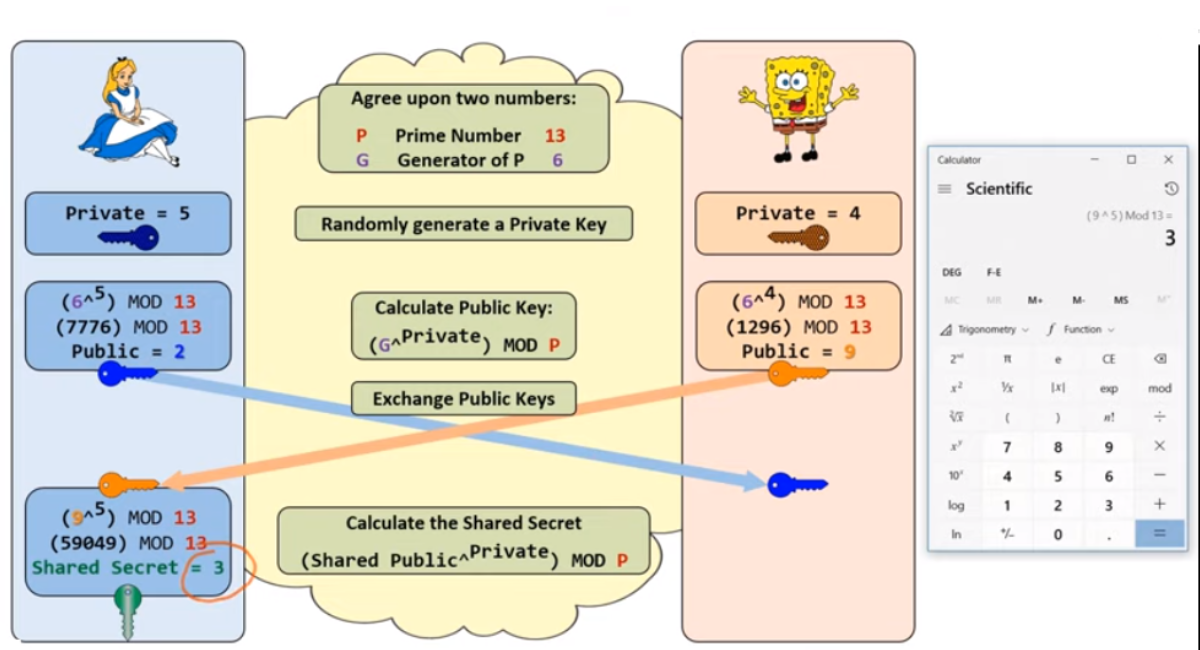
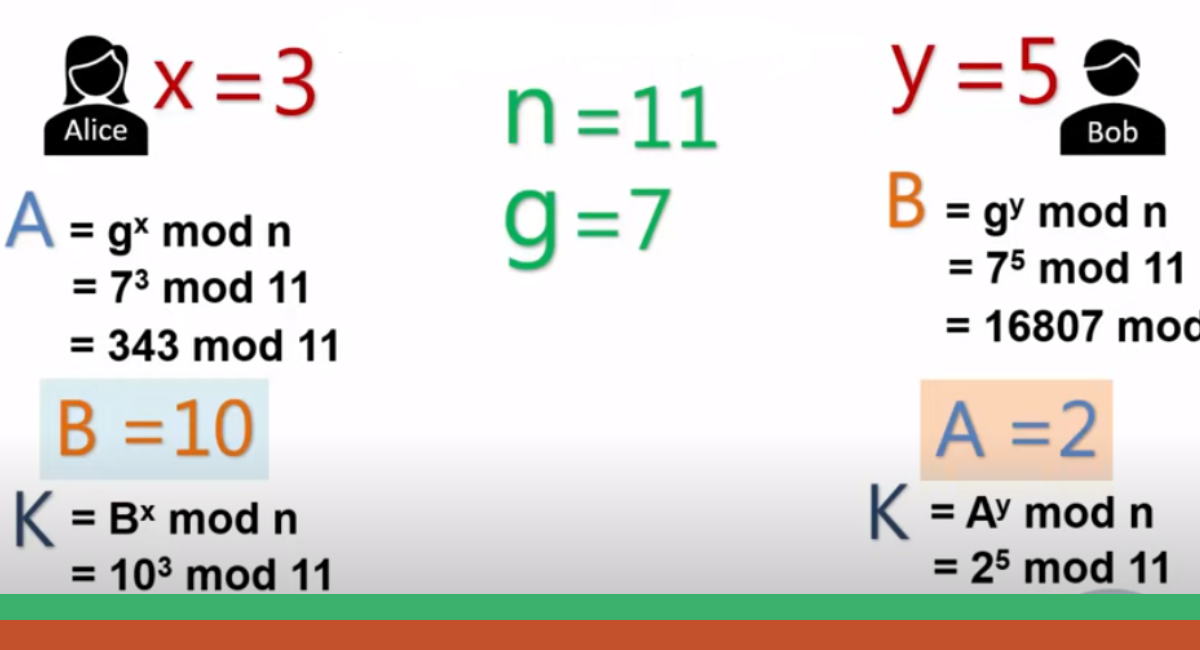
1. Public and Private Keys: Each party involved begins by choosing a private number (private key). They then compute a public number (public key) derived from this private key using specific mathematical operations.
2. Exchange of Public Keys: The parties exchange public keys over the insecure channel. Crucially, while the public key is derived from the private key, the private key cannot feasibly be deduced from the public key due to the computational difficulty of specific mathematical problems.
3. Generation of the Shared Secret: Each party uses its private key and the other party’s public key to generate a shared secret. This process ensures that both parties produce the same shared secret without ever having to exchange their private keys.

Security Implications

The magic of Diffie-Hellman lies in its ability to thwart eavesdroppers. Even if malicious actors intercept the public keys during transmission, they cannot derive the shared secret. The reason for this security is the underlying ‘discrete logarithm problem,’ a mathematical challenge that, to date, lacks a practical solution. In layman’s terms, while it’s straightforward to perform the mathematical operations in one direction (creating the public key from the private key), reversing the process (deriving the private key from the public key) is computationally unfeasible.

Applications of Diffie-Hellman

The Diffie-Hellman Key Exchange is a foundational part of various cryptographic protocols. Some prominent applications include:

1. Secure Shell (SSH): A protocol for securely accessing remote systems. SSH employs Diffie-Hellman to establish a secure channel over an insecure network.
2. Transport Layer Security (TLS): The protocol responsible for the ‘lock’ icon in your web browser. TLS uses Diffie-Hellman to ensure that your connection to a website is encrypted and secure.
3. Virtual Private Networks (VPNs): VPNs, tools for creating a secure connection over a public network, often rely on Diffie-Hellman to initiate the secure link.

Variants and Enhancements

The original Diffie-Hellman has given rise to several improved or specialized variants:

Elliptic Curve Diffie-Hellman (ECDH)

This uses elliptic curve cryptography to provide the same security levels as traditional Diffie-Hellman but with shorter key lengths. Shorter keys mean faster computations, translating to quicker and equally secure communications.

Authenticated Diffie-Hellman Key Agreement

This variant provides a shared secret and ensures the authenticity of both parties involved. It’s a mechanism to prevent Man-In-The-Middle attacks.

Contemporary Challenges and Considerations

Quantum Computing

A significant challenge for Diffie-Hellman (and many cryptographic systems) is the rise of quantum computing. Quantum computers could, in theory, solve the discrete logarithm problem quickly, breaking the security of Diffie-Hellman. Research is ongoing to develop ‘quantum-safe’ cryptographic methods.

Key Length

As computational power grows, the length of the keys used in Diffie-Hellman must also increase to maintain security. Therefore, systems need to update and adopt longer key lengths over time.

Key Takeaways

1. Fundamental Understanding: Diffie-Hellman Key Exchange is a cryptographic method that allows two parties to independently create a shared secret while communicating over an insecure channel.
2. Historical Significance: Introduced by Whitfield Diffie and Martin Hellman in 1976, this method revolutionized the cryptography field by allowing for secure key exchange without directly sending the key.
3. Core Mechanism: The technique relies on each party having a private and public key. They exchange public keys and use them with their private keys to generate the same shared secret.
4. Security Underpinning: The security of Diffie-Hellman is rooted in the ‘discrete logarithm problem,’ making it computationally infeasible to deduce private keys from exchanged public keys.
5. Widespread Applications: The Diffie-Hellman Key Exchange is a foundational component in SSH, TLS, and VPNs, securing countless online communications and transactions.
6. Variants: Beyond the traditional Diffie-Hellman method, enhanced variants like Elliptic Curve Diffie-Hellman (ECDH) and Authenticated Diffie-Hellman Key Agreement offer specific advantages.
7. Future Challenges: The rise of quantum computing challenges Diffie-Hellman’s security, necessitating ongoing research into ‘quantum-safe’ cryptographic methods.

FAQs

What is the primary purpose of the Diffie-Hellman Key Exchange?

The primary purpose is to allow two parties to generate a shared secret for encrypted communication without ever exchanging secret data.

How does Diffie-Hellman ensure security during the key exchange?

It banks on the ‘discrete logarithm problem,’ which means while it’s easy to compute in one direction (generating public from private keys), it’s computationally challenging to reverse.

Where is Diffie-Hellman typically used?

It’s used in cryptographic protocols such as SSH for accessing remote systems, TLS for secure web browsing, and VPNs for secure online connectivity.

How does the Elliptic Curve Diffie-Hellman (ECDH) differ from traditional Diffie-Hellman?

ECDH uses elliptic curve cryptography, providing similar security levels as the traditional method but with shorter key lengths, leading to faster computations.

Why is there concern about quantum computing regarding Diffie-Hellman?

Quantum computers have the potential to solve the discrete logarithm problem quickly, which would compromise the security offered by the Diffie-Hellman Key Exchange.

Do both parties generate the same secret in the end?

Even though they never directly exchange their private keys, both parties will independently arrive at the same shared secret using the Diffie-Hellman method.

In Conclusion

The Diffie-Hellman Key Exchange is a game-changer in the realm of digital security. Its elegant approach to creating a shared secret over an insecure channel laid the groundwork for many secure communications we take for granted today. (newportworldresorts.com)

In an era where digital communication dominates, and cybersecurity threats continually evolve, it’s essential to appreciate and understand the tools that keep our data safe. While devised in the 1970s, the Diffie-Hellman algorithm remains a crucial pillar in the architecture of modern cryptography.